Python. Операции с множествами

Рассмотрим операции с множествами.

Пусть дано два множества, с которыми будем проводить эксперименты.

Множества заключаются в фигурные скобки {}. Множества содержат только уникальные значения. Нельзя в множестве иметь два раза одно и тоже число.

Если множество задается сразу, то можно сразу его записать в фигурных скобках

a={5,9,3,1}

если множество пока пустое, тогда пишем так:

a = set()

 

Добавление элемента
a.add(12)

print(a)

Вывод:  {1,3,5,9,12}


# Удаление значения
a.remove(3)
print(a)
Вывод:  {1,5,9,12}

# Проверка на наличие значения - есть ли 5 в множестве
print(5 in a)  
Выведет: True

• remove(): Удаляет указанный элемент. Если элемента нет в множестве, возникает ошибка KeyError.
• discard(): Удаляет указанный элемент. Если элемента нет в множестве, ничего не происходит.
• pop(): Удаляет и возвращает случайный элемент из множества. Если множество пусто, возникает ошибка KeyError.
• clear(): Удаляет все элементы из множества.

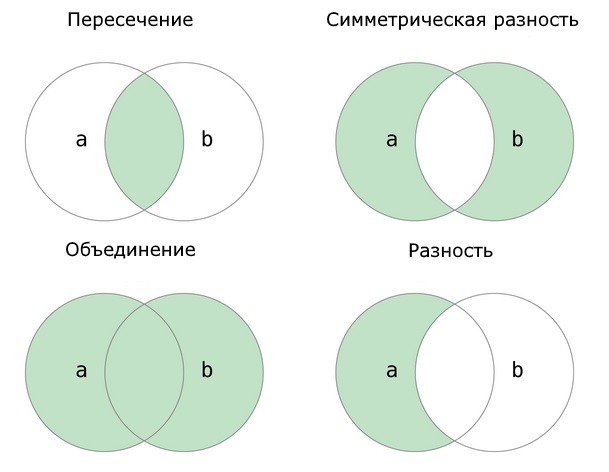
ОПЕРАЦИИ С МНОЖЕСТВАМИ
Где красное - такой будет ответ.

Например множества 
a = {3,5,2}
b={7,6,3}

| - это union, объединение

a | b будет {2,3,5,6,7}

u = a | b
print(u)
Видим что при объединении все красное, значит ответ будет все значения, только повторяющиеся будут включены 1 раз. Если две тройки, в 
объединенное множество войдет только одна тройка.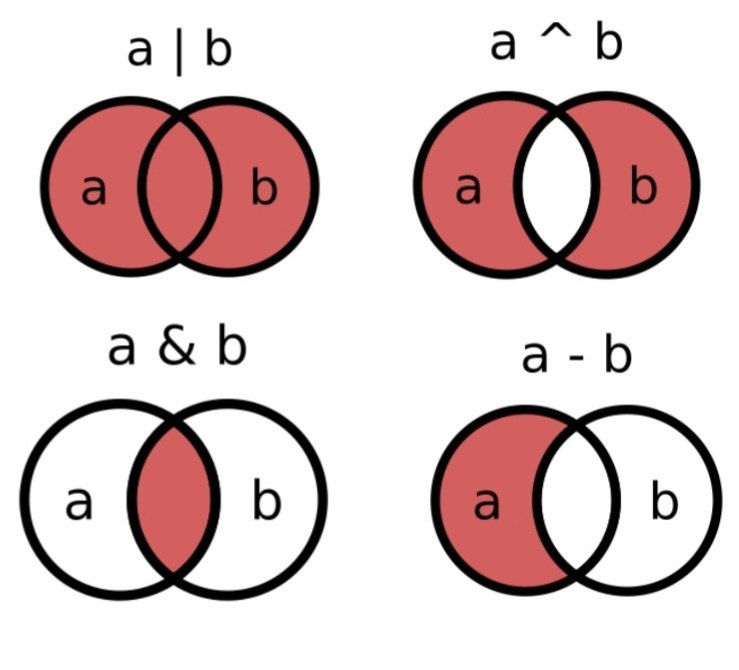

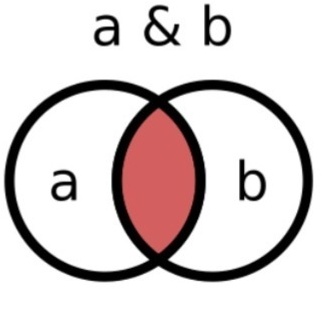
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ &

a = {3,5,2}
b={7,6,3}

Логично что будет вывод только одинаковых элементов.

А так как здесь только 3 встречается в обоих множествах, то выведется ответом 3.

p = a&b

print(p)

Вывод: {3}

 

РАЗНОСТЬ МНОЖЕСТВ “-“

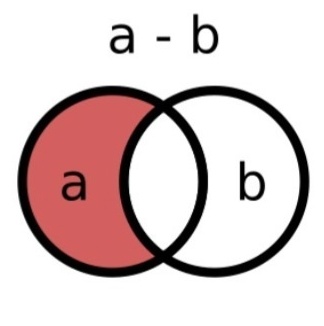
По картинке видно, что ответом будут значения из первого множества, которых нет во втором.

a = {3,5,2}
b={7,6,3}

r=a-b

Выведет {5,2}

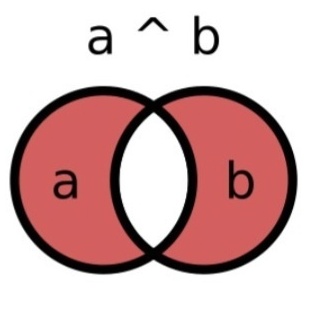
СИМЕТРИЧНАЯ РАЗНОСТЬ ^

a = {3,5,2}
b={7,6,3}

r=a^b

Выведет {2,5,6,7}

 

КАК СРАВНИТЬ МНОЖЕСТВА

print(a==b)

 

ЯВЛЯЕТСЯ ЛИ МНОЖЕСТВО А ПОДМНОЖЕСТВОМ B

a.issubset(b)

Другой вариант использовать <=
a<=b
если a входит в b, то ответ будет True

МНОЖЕСТВО НЕ ПУСТОЕ?
len(a) 
Выведет 0, если пустое