Популярно о мультибитном ЦАП

Когда речь заходит о хорошем качестве, точнее натуральном, звучании, то неизменно слушатели разделяются на приверженцев мультибитных и однобитных цапов. На самом деле разница в звучании на много больше зависит от реализации обвески после самой микросхемы, и однобитные ЦАП, дельта-сигма, появились позже, как развитие идей цифрового звука и потенциально более современны. Тем не менее и мультибитные и однобитные ЦАП долгое время развивались параллельно. Правда вероятно это сосуществование закончилось не в пользу мультибита, вероятно последний из могикан мультибитный PCM1704 снят с производства. Да и стоил он в последнее время негуманно и несоразмерно со своими возможностями — 70 долларов извините меня, это не 10 и не 20 долларов за чип, а если таких чипов в устройстве 8?

Denon DCD-S1 на 4х мультибитах PCM1704 высшего грейда К.

Я слушал устройства и на 8 мультибитных PCM1704 и на четырех PCM1704, и 8 мультибитных TDA1543, и, разумеется, на однобитных дельта-сигмах — PCM1794, CS4398, AK4490.

Бывают хорошо играющие устройства и с недостатками. если в каком то мультибите есть характерные «недостатки» или «особенности» звучания, то при прослушивании вы сможете отгадать какого именно типа цап играет, но если цап реализованные близко к эталонному, методом отгадывания у вас уже ничего не выйдет, оба представителя будут звучать очень хорошо. Другим словами, да, я отличу на слух, когда будет играть 8 штук TDA1543, но я легко попутаю с дельта-сигмой 8 штук PCM1704.

TeraDak на 16 мультбитных чипах TDA1543

Поэтому сильно заморачиваться именно на «мультибит» или «однобит» не стоит — это не имеет значение. Стоит заморачиваться именно моделью цап и его реализацией.

Например, PCM1794 или Sabre ES9018 точно очень хорошие ЦАП, но что из них вышло в конкретном изделии нужно слушать. Хотя задел все равно они делают намного лучший, чем если бы это был ЦАП на микросхемах более простого уровня.

Тем не менее, я думаю, что многие не очень понимают, что же такое мультибит и однобит. Кто из них лучше я уже ответил — никто, нужно слушать реализацию. А вот как что устроено, об этом сегодняшний разговор.

Для начала выясним, что же такое МУЛЬТИБИТ или мультибитный ЦАП.

Одна из мультибитных легенд PCM63 (20 bit)

Я сразу поясню, что я не не специалист в этой сфере и всю информацию, в силу своего понимания почерпнул из книг и доступных источников и пересказываю так, как  я это понял. Если вы заметили неточность или неверное объяснение — не стесняйтесь, поправьте меня в комментариях, сделаем объяснение точнее и понятнее для всех.
Мультибитным цапом, наверное обычно, называют  цап на основе резистивной R-2R матрицы.
Что это значит?
Банально то, что звук мы получаем просто благодаря резисторам по особой схеме.
Цапы этого типа самые древние — это TDA1540, TDA1541, TDA1543, CXD20017, CXD890, PCM63, PCM58, PCM1704 и тд.
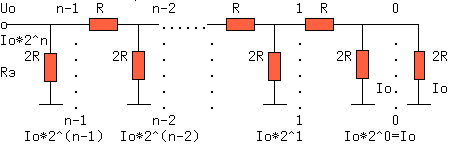
Ниже я приведу одну простейшую схему по которой вы возможно поймете что такое R-2R матрица, и почему именно R-2R.
Т.е. уже сейчас по описанию ясно что стоит один резистор c наминалом, пусть 180 Ом, апосле него идет резистор с номиналом в 2 раза больше, т.е. 2R.

Если R=180 Ом, то 2R= 180*2=360 Ом.
Смотрим схему:

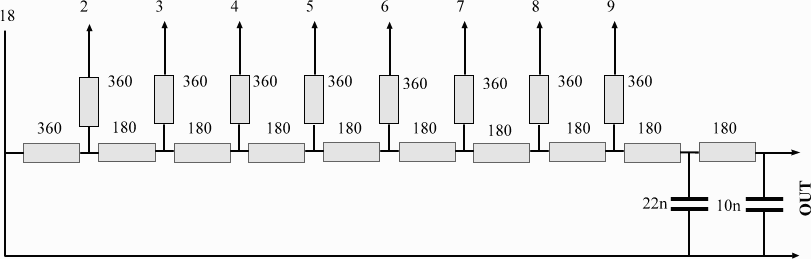
Посчитаем количество вертикальных резисторов номиналом 360 Ом. Их 8.
Да, на картинке приведена схема 8-битного цап лестничного типа, R-2R матрица.
Как мы можем получить больше бит? Доставить больше вертикальных резисторов. Чтобы стало 16 бит, их должно быть 16 + от них отойдут по 2 резистора в стороны, как елочка.
Вы можете не поверить (а возможно кто то легко узнал эту схему), но это реально работающая и популярная в старые времена схема монофонического 8-битного (мультибитного) ЦАП.
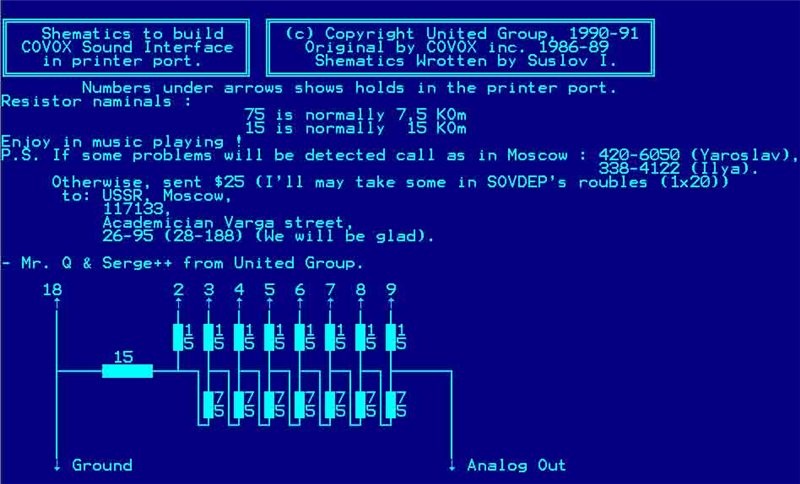
Если еще не догадались, то приведена схема звуковой «карты» Covox подключавшейся в LPT-порт компьютера и позволявшей слушать относительно качественную музыку или слышать аудиосопровождение в играх.
Выводы 18,2,3,4,5,6,7,8,9 на схеме — это контакты разъема LPT (принтерного) порта, с которых приходил цифровой сигнал в этот ЦАП, где и преобразовывался в  звук (выход по току или напряжению (при инверсном варианте) в зависимости от схемы)  .

Самодельный Covox, ЦАП на R-2R матрице

Вы и сегодня можете спаять такой самодельный цап, вам понадобятся только резисторы двух номиналов. Один номинал должен быть выше другого в 2 раза (матрица же R-2R).
Например? если вы выбрали резисторы на 7,5кОм, то к ним в компаньоны нужен резистор на 15К.

Или если взяли на 10К, то для лестницы нужен резистор 20К.
Номиналы могут быть разные, но от их значения зависит, насколько громким будет выход с ЦАП.  Чем больше значение резисторов, тем тише звук на выходе.
Но вам наверное не очень понятен принцип работы такого ЦАП.
Принцип работы следующий, каждый из «вертикальных» резисторов — это «бит».
Почему такие цап называются мультибитами?
Посмотрите, у нас 8 резисторов расположенных вертикально, представьте, что это трубки в которые могут течь данные.
Так как у нас есть 8 трубок, то данные мы можем заливать сразу одновременно в 8 трубок.
В одну трубку потекло, во вторую, в третью, и тд — и в сумме мы получаем максимальный ток. Если в какую то трубку не потекли данные, то сумирующий  ток будет ниже. Может не потечь и в 2-3 и более трубок, и на выходе будет ток другой.
Из этого следует, что мы получаем звук.
Но как определить в какую»трубу» или ножку резистора что течет.
Тут самое простое. Т.к. наш цап 8-битный. Т.е. 1 бит может иметь значение 0 или 1. Обозначается он так 2 в степени такой то. Биты располагаются от младшего к старшему.  С правой стороны биты имеют меньшее значение, а с левой — большее.
Каждый бит имеет значение в зависимости от своего расположения в ряду.
Так как у нас всего 8 бит в Covox, значит максимальное значение у нас 2 в степени 8.

2^8=256
Да, 2 в степени 8 может содержать 256 значений.

Самое большое число, когда все биты установлены в 1.
Т.е. самое большое 8 битное число — это 11111111 — все биты установлены в 1.
Видите 8 единиц. Это означает число 256.
Как?
Бит у нас в данном случае всего 8. Крайний правый бит называется нулевой, чуть левее — первый, еще левее — второй и тд.
Вот так (верстка может сбиться):

Расположение     7 6 5 4 3 2 1 0
Биты                     1 1 1 1 1 1 1 1

Значение бита зависит от его расположения.

Самый правый бит под номером 0 считается как
2^0 (два в степени 0)=1

Левее него бит под номером 1 считается как 2 в степени 1
2^1 = 2
^ — это значек степени

Следовательно следующий бит — по номеру расположения 2 имеет значение
2^2=4
и далее

2^3=8
2^4=16
2^5=32
2^6=64
2^7=128

Если сложить все эти результаты 1+2+8+16+32+64+128=256 — максимальное значение для 8 бит.

Для 16 бит соответственно максимальное число 2^16=65536.

Теперь смотрите — есть двоичное восьмибитное число

01010011

Нули игнорируем, смотрим по расположению битов, у нас с единичкой биты по номерами 0,1,4 и 6 (смотрим с права налево).

Если непонятно, то продемонстрирую
Расположение   7 6 5 4 3 2 1 0
Биты                   0 1 0 1 0 0 1 1

Сверху указан номер расположения бита, он же является степенью в которую нужно возвести 2 (2 — потому что двоичный код, есть 0 или 1 значение, т.е. всего два значения у бита).
Ну и теперь легко посчитать реальное число в привычной нашей системе счисления.
Переведем двоичный код, который принимает цап на входе в число, которое может быть как точным значением величины тока или напряжения, так и процентным соотношением оного.

Значит у нас активированы единичкой биты 0,1,4 и 6.

Считаем
2^0+2^1+2^4+2^6=1+2+16+64=83

Т.е. двоичное число 0 1 0 1 0 0 1 1  — это десятиричное 83. Ну например 83мА.

И вот это число ввиде нулей и единичек подается на цап.
Теперь представьте, что вот эти 0 и 1 — это ток подающийся или не подающийся на резисторы в цап.
вот резисторы | | | | | | | |
вот наше число 0 1 0 1 0 0 1 1

Где стоит единичка, на резистор подастся ток, где 0 — ничего не подается.
А далее благодаря лесенке из резисторов R-2R мы получаем аналог того, как мы получали десятичное число из двоичного. Следующий резистор, это как следующий разряд у числа будет увеличивать ток на определенную величину, а на выходе ЦАП это все просуммируется.
В следующее мгновение на цап подастся другое двоичное число закодированной музыки, и оно так же будет преобразовано в реальное абсолютное или процентное значение тока.
Вы заметили что мы говорим о 8 битах.
Вы знаете что стандарт СД-диска — 16 бит.
Это всего лишь больше резисторов в матрице, не 8 штук R+2R, а 16 штук R+2R. Так же можно и больше сделать.
Но тут есть некоторая дилема, тормоз этой идеи.
Мы знаем, что должны сумvироваться только токи/биты со значением 1. Чем больше бит, тем больше лестниц и больше сопротивление, и значение младшего бита после стольких сопротивлений может быть настолько ничтожно, что сомнительно само увеличение битности в такой матрице.
Из схемы Covox видно, что самый младший бит может повлиять меньше всех на выходной сигнал, ему приходится преодолеть цепочку из максимального количества сопротивлений, следующий бит достигает выхода быстрее, и т.д. Чем больше бит у ЦАП, тем меньше значение у самого младшего бита (по моему это называется весом).
Производители по этой технологии доехали до 20 бит. Дальше сложная борьба с шумами и очень минимальные значения младшего бита сводят все на нет.
Главная трудоемкость производства — это подбор идеально точного номинала резисторов — они подгоняются как можно точнее лазером — есть такая технология (или уже была). Если резисторы будут иметь значение не очень точное, то с верным трактованием двоичного кода придется распрощаться — результат будет привирать. Так же отмечалось, что у таких цап, как R-2R плохая монотонность и точность.
Поэтому очень скоро мысль пришла к однобитным, более точным ЦАП. После моего пространного объяснения мультибитового цап, я думаю вы себе уже нарисовали картинку, что если 16 битный цап, это 16 резисторов от которых резистивная матрица формируется, то в 1-битный подается в единицу времени всего 1 бит. Как это работает? Интересный вопрос, но в данной публикации я не буду пытаться объяснить принцип работы более совершенного технически и одновременно и простого и сложного однобита.
Тема этого материала — мультибит.

Возможно из моего объяснения принципа работы мультибитного ЦАП вы ничего не поняли, поэтому я приведу выдержку взятую с другого интернет-ресурса (простите, но не могу сейчас уже узнать откуда):
«Принцип работы мультибитного ЦАП очень прост — резисторы представляют собой многовходовой каскад простейших делителей напряжения, где каждый вход соединяется или с напряжением питания или с корпусом(висеть в воздухе вход не может).
Причем напряжение на каждом входе дает один и тот же прирост напряжения на выходе делителя, вне зависимости от комбинации напряжений на других входах. Конечно другие тоже влияют но каждый вход имеет свой «вес», то есть дает свою прибавку к выходному напряжению. Максимальную прибавку дает старший разряд, в нашем случае вход, соединенный с контактом 9 LPT, «вес» этого входа, т.е. прибавка которую дает этот вход — 0,5 напряжения на контакте 9, или для логических уровней — 2,4 — 2,5 Вольта. «Вес» входа, соединенного с выводом 8 равен 0,25 напряжения на контакте 8, вес входа соединенного с выводом 7 — 0,125 от входного напряжения. И так далее. Чем младше разряд, тем меньшую прибавку к выходному напряжению он дает.»

Настоящие флагманские ЦАП устроены безусловно несколько посложнее, но работают на описанном принципе резистивной матрицы R-2R.
От себя я могу только добавить, что раз уж мы рассмотрели, как перевести двоичный код в десятеричный, то стоит показать и обратный процесс. Он выглядит так.
Нужно делить десятеричное число на 2. И смотреть на остаток. Остаток будет 0 или 1 — это и есть искомый двоичный код.
Например приведем к двоичной форме число 29
29/2=14 остаток 1
14/2=7 остаток 0
7/2=3 остаток 1
3/2=1 остаток 1
1
А так как последнее значение 1 уже на 2 не разделить, то его тоже включаем в число.
Число записывается задом наперед, т.е. начиная с последнего значение и далее

11101

Если число 8 битное, то с левой стороны добавляем нужное количество нулей, чтобы чисел было всего 8
00011101
Если число 16 битное, то добавляем с лева нулей столько, чтобы было всего 16 чисел
0000000000011101
Проверим верно ли мы перевели число 29 в 11101
степени 43210
число 11101
Значение есть у битов 0,2,3 и 4.
2^0+2^2+2^3+2^4=1+4+8+16=29

Еще одна картинка показывающая принцип расчетов, где считается другое значение:

Надеюсь тема двоичных чисел и мультибитных ЦАП немного стала понятнее. Как видим в мультибитных цап нет никаких космических технологий, где корабли бороздят просторы мирового, технология эта древняя и несовершенная. Сами понимаете с ростом мощностей железа и увеличением скоростей обработки информации рано или поздно мультибит так итак должен был уступить место более совершенным технологиям.

Есть что сказать по теме мультибитных ЦАП? Обсудить эту публикацию можно у нас на сайте перейдя по этой ссылке.

Для тех кому недостаточно объяснений: